Research Associate: Dipl.-Ing. F. Keller
Motivation
In the field of Chemical Engineering the material structure is an important parameter. Especially the pore structure is a key property for many processes and products. Examples thereof are:
- Open-porous membranes, e.g. dialysis membranes, where a defined pore structure is needed for the separation of molecules by steric effects

Figure 1 : Evolution of the porous structure of a membrane by phase inversion [Strahtmann 1979]
- Heterogeneous catalysts and adsorbent materials, where an open-porous structure is needed for accessibility of the active sites

Figure 2 : Generation of a porous transport network by decompositon of wax
Despite the widespread use of such materials, the manufacturing is almost completely based on experimental experience and empirical correlations. Therefore a model based development and design is desired to alleviate the extensive trial and error process. So far only simplified models exist, mostly based on:
- Idealized geometry
- One-dimensional heat and mass balances
- “effective” parameters and transport equations
Due to the mentioned limitations of the existing models, no prediction of the evolving porous structure is possible.
Objective
The objective of the presented project is the prediction of the resulting morphology by detailed description of the underlying physical and chemical processes during the generation on an open-porous system. By comparing the obtained results with experimental data, the model quality will be enhanced in an iterative manner.
Methods
For modeling the morphogenesis to an open-porous material, several processes have to be considered. The most important are depicted in the figure below.
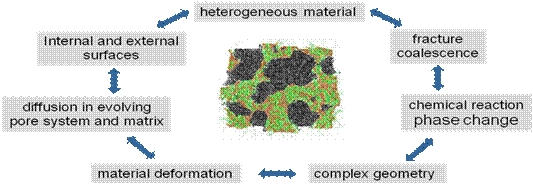
Figure 3 : relevant single processes for structure formation
These complex and coupled systems are difficult to describe by mesh-based methods. Especially difficult is the treatment of evolving interfaces, material fracture as well as the formation and coalescence of voids. These phenomena can be handled in relative ease by particle methods. The method for this project is the so called Smoothed Particle Hydrodynamics (SPH) method, invented by Gingold and Monaghan [1] as well as Lucy [2].
The advantage of SPH lies in the canonical derivation of the methods form the laws of continuum mechanics. The continuum is discretized by particles. Any distributed variable can be represented by a kernel approximation, which can be transformed to a weighted sum of the variable of the neighbor particles.
![]()
The approximation of a derivative can be done by the exact derivation of the approximated function.
![]()
Modeling the overall process
In the following a simple example of the formation of an open-pore is shown at different time steps. The computational domain is shown in the first picture, with black particles mimicking zeolite particles (elastic material behavior). The yellow particles depict wax particles which react with oxygen to decomposition products. The red particles represent polymeric material with viscoplastic material behavior. The diffusion of oxygen from the exterior gas phase through the polymer matrix is included as well the decomposition of wax by chemical reaction to a gaseous blowing agent. With the extent of the reaction, pressure is built up in the void, causing the pore to grow. The process is ended after pressure compensation with the outside as soon as the pore opens up.

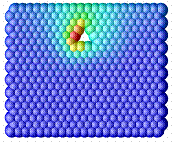
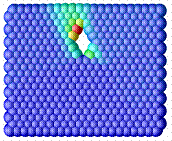
Figure 4: left: computational domain, center: wax decomposes, right: shear rate exceeds viscoplastic yield stress
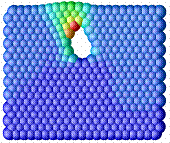
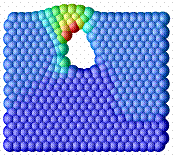
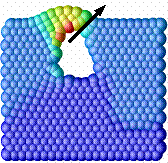
Figure 5: left: plastic flow of polymer, center: void growth be internal pressure continues, right: open pore is formed, pressure compensation with the outside through the open pore (arrow).
-
R. A. Gingold, J. J. Monaghan
Smoothed particle hydrodynamics: Theory and application to non-spherical stars
Mon. Not. Roy. Astron. Soc., Jg. 181, S. 375 -
L. B. Lucy
A numerical approach to the testing of the fission hypothesis
Astronomical Journal, Jg. 82, S. 1013–1024

